3.11 - Adiabatic Processes
Adiabatic Cooling
Watch: Instructor's Lecture Links to an external site.
The only way that large air masses are cooled to dew point to form clouds is by the expansion in rising air. This is adiabatic cooling. When air rises, its pressure drops, so it expands and cools. If it rises far enough, it cools to dew point temperature. This triggers condensation around nuclei and the formation of clouds.
If we measure the rate of cooling that occurs in an air mass that is actively rising, air will cool at a relatively steady rate of -5.5°F/1,000 feet. This is the dry adiabatic lapse rate. As the rising air cools, it can "hold" less moisture and its relative humidity increases. If the air rises high enough and cools enough it reaches dew point temperature, the relative humidity is 100% and condensation occurs. The altitude at which this occurs is the lifting condensation level and when we look up at the base of clouds that's the altitude we are seeing.
As soon as dew point temperature is reached, condensation begins and latent heat is released. This slows the rate of cooling to -3.3°F/1,000 feet. This is the wet adiabatic lapse rate. After the air is cooled to dew point temperature, as long as it continues to rise, the air will cool at the wet adiabatic lapse rate.
When air descends, it is being compressed and warming. As it warms, its relative humidity drops. Air masses that are descending, warm at +5.5°F/1,000ft as long as they are descending.
Expansion and adiabatic cooling in rising air explains why low pressure is associated with clouds and precipitation. Compression and adiabatic warming in descending air explains why low pressure is associated with clear skies.
Adiabatic Cooling Problems
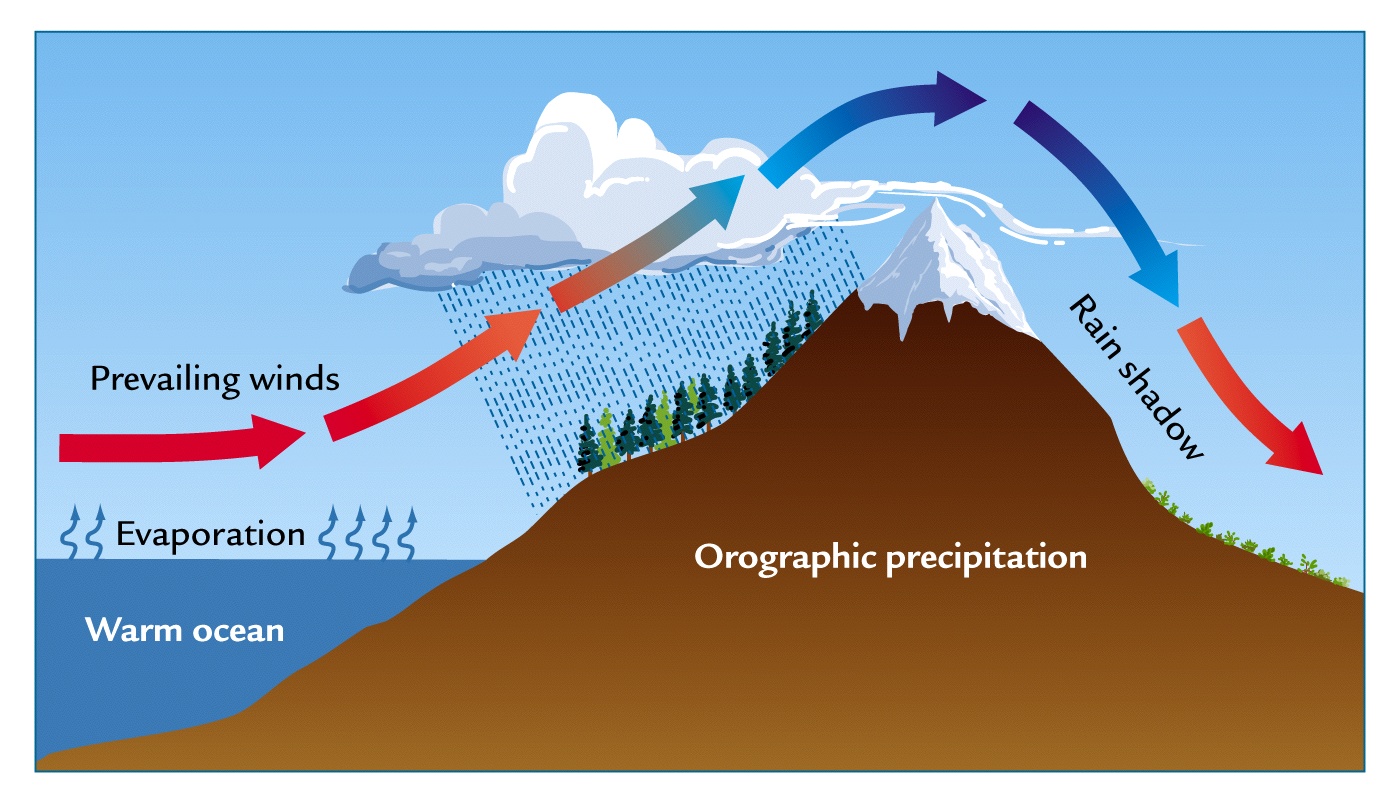
Air masses are forced to rise for several reasons: in low pressure, in convective lifting (hot afternoon over a beach) or orographically (air is forced to rise over a mountain). Knowing the adiabatic lapse rates we can calculate what happens to temperature in rising and descending air.
For adiabatic process questions, we usually use air rising and descending over a mountain as an example. It has the advantage of being easy to visualize. But remember, any time air rises for any reason this process is at work. In order to calculate what is happening in rising and descending air, I will always give you (or you will be able to find out) the following pieces of info:
- The starting temperature of the airmass that is rising
- The elevation of the mountain
- The dew point temperature
You will always be asked the following questions:
- At what altitude does the air cool to dew point
- What is the temperature at the top of the mountain
- What is the temperature at the bottom of the mountain after the air has descended.
I ask that you draw your self a simple mountain and put in the relevant information. It makes the problem easier to visualize.
Problem - The mountain is 10,000 feet tall. The air rising over the mountain starts at 80°F. The dew point temperature is 47°F. Let's go through the steps to answer the questions above.
Step 1. - First lets find out how many degrees the air would have to cool to reach dew point.
Start with the temperature of the rising air (80°F)and subtract it from the dew point temp (47°F)
80 - 47 = 33. The air would have to cool 33°F to reach dew point
Step 2 - How many thousand feet would the air have to rise to cool 33°F?
Take 33 and divide it by the rate of cooling, the dry adiabatic lapse rate (-5.5°/1000 ft)
33/5.5 = 6. This 6 is 6,000 feet. (The 6 is referring to the number of 1000 feet). So at 6,000 feet the air has cooled to dew point
Step 3 - The air still must rise another 4,000 ft to the top of the mountain (10,000 ft). But its rate of cooling has slowed because dew point was reached, and condensation has occurred releasing latent heat. It now cools at -3.3°F/1,000 ft (the wet adiabatic lapse rate)
Take how many thousand feet the air must still rise to get to the top of the mountain, (4),000 feet and multiply it times the wet adiabatic lapse rate (3.3) (Get rid of the zeros to do your calculation)
3.3 x 4 = 13.2°F. the air will cool another 13.2°F after it reaches dew point as it rises to the top of the mountain
Step 4 - What is the temperature at the top of the mountain?
The air cools 13.2°F from the dew point temperature of 47°F at 6000 feet. Subtract these numbers for the temp at the top of the mountain.
47 - 13.2 = 33.8°F is the temperature at the top of the mountain
Step 5 - What happens as the air descends down the other side? It warms at +5.5°F/1000 ft
Multiply the rate at which the air warms (5.5°/1000ft) times the number of feet ( 10, 000 - minus all those zeros)
10(000) x 5.5 = 55°F. The air warms 55°F from the top of the mountain to the bottom of the mountain
Step 6 the last step....What is the temperature at the base of the mountain?
The air warms 55°F from the temperature at the top of the mountain (33.8°F) , so we add!
55 + 33 = 88.8°F. The air is 88.8°F at the bottom of the mountain
Make sure you watch this week's video for more information on doing these problems. You will do them in homework, on an exam and on an extra credit assignment so make sure you are clear about how to do them.